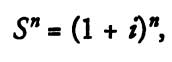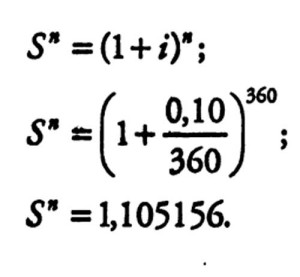При определении «ставки дохода на инвестиции- как основного финансового критерия во внимание следует принять эффект сложного процента. Сложный процент означает, что уже полученный процент, будучи положенным на депозит вместе с первоначальными инвестициями, становится частью основной суммы. Поэтому в следующий период наряду с первоначальным депозитом он также приносит новый процент. Напротив, простой процент не предполагает получения процента на процент.
Например, предположим, что 100 долл. депонированы на счет, ставка по которому составляет 10% и этот процент накапливается раз в год. В первый год 100 долл. принесут 10 долл. процента (10% от 100 долл. = 10 долл.). В конце первого года остаток составит 110 долл. (100 долл. + 10 долл. = 110 долл.). Если в течение второго года вся сумма в 110долл. будет оставаться на депозите, то во второй год процент составит уже 11 долл. (10% от 110 долл. = 11 долл.). По истечении 5 лет остаток составит уже 161,05 долл. при условии, что весь процент остается на депозите. Это показано в табл. 3-1. Для сравнения: при простом проценте ежегодный доход на инвестиции составит 10 долл.; поэтому через 5 лет накопленная сумма будет равна 150 долл. (100 долл. + 5 X 10 долл. = 150 долл.), что также видно из таблицы
Депозит 100,00 долл. — сложный и простой процент (ставка = 10%)
| Год | ‘ |
Сложный |
Простой |
|
процент |
процент | ||
|
0 |
Депозит |
100,00 |
100,00 |
|
1 |
Подученный процент |
10,00 |
10,00 |
|
1 |
Остаток, конец года |
110,00 |
110,00 |
|
2 |
Полученный процент |
11,00 |
10,00 |
|
2 |
Остаток, конец года |
121,00 |
120,00 |
|
3 |
Полученный процент |
12,10 |
10,00 |
|
3 |
Остаток» конец годя |
133,10 |
130.00 |
|
4 |
Полученный процент |
13,31 |
10,00 |
|
4 |
Остаток, конец года |
146,41 |
140,00 |
|
5 |
Полученный процент |
14,64 |
10,00 |
|
5 |
Остаток, конец года |
161,05 |
150,00 |
Сила сложного процента может быть показана на следующем примере. Если бы индейцы, продавшие в 1626 г. остров Манхэтген Питеру Миньюту за товары стоимостью 24 долл., инвестировали эти 24 долл. под ежегодно накапливаемые 6%, то в 1983 г. сумма этих вложений составила бы почти 26 млрд.долл. Если бы индейцы инвестировали под ежегодно накапливаемые 7%, то остаток достиг бы астрономической суммы 741 млрд.долл. В то же время, при 6%-ной простой ставке за тот же период времени 24 долл. превратились бы только в 538,08 долл., при 7%-ной простой стаэке — только в 23,76 долл.
Логика сложного процента очевидна. Все деньги, которые оставлены на депозите, должны приносить процент, Более того, процент приносят только те деньги которые оставлены на депозите. Эту инвестиционную логику необходимо твердо усвоить всем финансовым аналитикам и оценщикам.
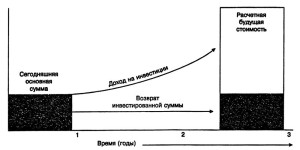
Рис. 3-1 показывает графически рост основной суммы сегодняшних вложений до расчетной будущей стоимости с учетом сложного процента.
Предварительно рассчитанные таблицы сложного процента
Поскольку сложный процент применяется очень часто и широко, инвесторы считают удобным и целесообразным воспользоваться стандартными таблицами, содержащими предварительно рассчитанные факторы сложного процента. Фактором (factor) называется одно из двух или более чисел, которые, будучи перемноженными, дают заданный результат, Если инвестор знает, какова будет стоимость 1 долл. к концу 23-го года при ежегодном накоплении 10%, то он также может узнать, какова будет стоимость 43,22 долл. — умножив 43,22 долл. на стоимость 1 долл. к концу 23-го года. Во всех таблицах сложного процента используется формула:
РОСТ ОСНОВНОЙ суммы по сложному проценту
где
Sn = сумма после п периодов;
i = периодическая ставка процента;
п = число периодов.
Большинство «шестифакторных» таблиц сложного процента показывает рост 1 долл. в колонке 1. В табл. 3-2 приведен пример таблиц сложного процента при ставке 10% и ежегодном накоплении. В том же случае, если начальный остаток больше (или меньше) 1 долл., для определения искомой суммы его просто следует умножить на табличный фактор. Например, если в течение пяти лет 10 000 долл. ежегодно приносят 10% (по сложному проценту), то к концу этого срока остаток составит 16 105,10 долл. (10 000 долл. X 1,61051 = 16 105,10 долл.).
Это происходит, поскольку каждый вложенный доллар приносит процент по одной и той же ставке. Через 5 лет каждый отдельно взятый доллар при ежегодном накоплении 10% вырастет примерно до 1,61 долл. Соответственно 10 000 долл. превратятся в 10 000 долл. X 1,61.
Правило 72-х
Правило 72-х, в основу которого положены логарифмы, использует число 72 для примерного расчета количества лет, необходимых для увеличения денежной суммы в два раза при том, что весь процент остается на депозите.
Накопленная сумма 1,00 долл. при ставке 10%
| Год |
Накопленная сумма 0 |
| 1 |
1,10 |
| 2 |
1,21 |
| 3 |
1,331 |
| 4 |
1,4641 |
| 5 |
1,61051 |
| б |
1,771561 |
| 7 |
1,948717 |
| 8 |
2,593742 |
| 9 |
2,357948 |
| 10 |
2,593742 |
| 20 |
6,727500 |
| 30 |
17,449402 |
| 50 |
117,390853 |
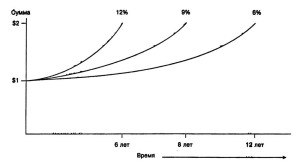
Согласно данному правилу, для того чтобы рассчитать этот срок необходимо разделить 72 на ставку процента, выраженную целым числом. Правило 72-х достаточно хорошо срабатывает при ставках от 3 до 18%. Например, при сложной ставке 3% денежная сумма удвоится примерно за 24 года (72 : 3 = 24) (при таком же простом проценте — за 33V3 лет). При ставке 4% деньги удвоятся за 18 лет, 6% — за 12 лет, 12% — примерно за б лет. Правило 72-х действует также и «в обратном направлении*. Если известно, что за шесть лет 10 000 долл. превратились в 20 000 долл., то сложная годовая ставка составляет примерно 12% (72 : 6 = 12). Если же 10 000 долл. удвоились за десять лет, то ставка равна примерно 7,2%. Данная зависимость показана на рис. 3-2.
Более частое накопление
Нередко период накопления короче года. Накопление может происходить ежедневно, раз в месяц, в квартал или в полгода. Обычно устанавливается номинальная годовая ставка, например 10%, однако при более частом накоплении эффективная ставка процента повышается. Общая формула остается той же:
однако с учетом сокращения периода накопления в нее должны быть внесены изменения.
При корректировке данной формулы число лет, на протяжении которых происходит накопление, умножается на его частоту в течение одного года; одновременно номинальная годовая ставка процента делится на частоту накопления. Результат покажет эффективную ставку процента за период накопления.
Правило 72-х — время, необходимое для увеличения денежной суммы в два раза при сложном проценте
Например, 10%-ная ставка при ежеквартальном накоплении в действительности означает, что процент будет выплачиваться по ставке 2*/2 % за квартал каждого года. Если накопление происходит ежемесячно, то выплачиваемый за месяц процент составит 0,00833 (0,10 :12 = 0,00833). Для более частых накоплений также построены расчетные таблицы. Табл. 3-3 показывает рост 1 долл. при 10%-ной ставке и ежеквартальном накоплении. Чем выше частота накопления, тем быстрее растет денежный остаток (см. табл. 3-4). Это означает, что эффективная годовая ставка будет выше (при более частом накоплении) номинальной годо&ой ставки.
Дискретное и непрерывное накопление
Термин дискретный (discrete) означает, что интервал накопления фиксирован, т. е. оно осуществляется раз в год, в квартал или месяц. Непрерывное накопление предполагает, что процент накапливается за возможно наиболее короткий период времени.
Рост 1,00 долл. при ежеквартальном накоплении (номинальная годовая ставка » 10%)
| Год | Квартал | Накопленная сумма (в долларах.) |
| 1 | 1 | 1,025 |
| 2 | 1,050625 | |
| 3 | 1,076891 | |
| 4 | 1,103813 | |
| 2 | 5 | 1,131408 |
| 6 | 1,159693 | |
| 7 | 1,188686 | |
| 8 | 1,2184029 |
Рост 1000,00 долл. при различных периодах накопления (номинальная ставка = 10%)
|
Период |
Сумма к концу |
Эффективная годовая |
|
накопления |
первого года (в долл.) |
ставка (в %) |
| Год |
1 100,00 |
10,00 |
|
Полугодие |
1 102,50 |
10,25 |
|
Квартал |
1 103,81 |
10,38 |
|
Месяц |
1 104,71 |
10,47 |
|
Неделя |
1 105,06 |
10,50 |
| День |
1 105,15 |
10,50 |
Хотя этот период является бесконечно коротким, более точным приближением непрерывного накопления является ежедневное накопление. При ставке 10% ежедневное накопление для «360-дневного года» может быть определено по следующей формуле, где Sn — сумма после п периодов:
Использование калькулятора для расчета по сложному проценту
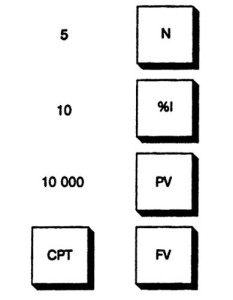
На клавиатуре большинства финансовых калькуляторов имеется ряд с пятью клавишами для финансовых расчетов. Клавиша N соответствует числу периодов. Клавиша %I — периодическая ставка процента; РМТ — периодический платеж; PV — текущая стоимость суммы и FV — будущая стоимость суммы. Кроме того, используется клавиша СРТ или COMPUTE — расчет.
При использовании сложного процента для определения единой будущей суммы по заданной ставке процента и через установленный временной интервал известны три переменные. Калькулятор позволяет найти четвертую. На некоторых калькуляторах предварительно должен быть установлен регистр CI (сложный процент).
РЯД клавиш финансовых расчетов
Результат: 16105,1 (на дисплее)
Рис 3-4. Клавиши калькулятора, используемые при расчете по сложному проценту. Ставка 10%, ежегодное накопление в течение 5 лет, первоначальная сумма равна 10 000 долларов
Результат: 16386,16 (на дисплее)
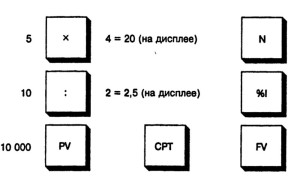
Рис. 3-5. Клавиши калькулятора, используемые при ежеквартальном накоплении. Ставка 10%, 5 лет (20 кварталов), первоначальная основная сумма равна 10 000 долл.
Например, для определения будущей стоимости 10 000 долл. при ставке 10% с ежегодным накоплением в течение 5 лет нажмите клавиши, показанные на рис. 3-4.
Та же задача, однако при ежеквартальном накоплении, может быть решена путем умножения числа лет на 4 с тем, чтобы учесть число кварталов, и деления ставки процента на 4, для того, чтобы учесть периодическую ставку процента. На рис. 3-5 показаны клавиши, используемые при ежеквартальном накоплении.
Источник: Джек Фридман, Николас Орудей. Анализ и оценка приносящей доход недвижимости.