Все шесть функций сложного процента строятся с использованием общей базовой формулы (l + i)n, описывающей накопленную сумму единицы. Все факторы являются производными от этого базового уравнения. Каждый из них предусматривает, что процент приносят деньги, находящиеся на депозитном счете, причем только до тех пор, пока они остаются на депозитном счете. Каждый из них учитывает эффект сложного процента, т.е. такого процента, который, будучи полученным, переводится в основную сумму.
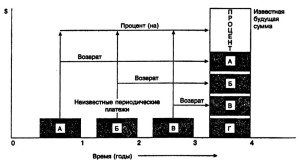
Рис. 4-5. Фактор фонда возмещения — графическое описание А, Б, В и Г — равные суммы, депонированные в конце каждого периода. Каждая сумма приносит сложный процент до тех пор, пока она остается на депозитном счете. По истечении рассматриваемого срока вкладчик может снять итоговую сумму. Фактор фонда возмещения рассчитывается таким образом, что последняя будет всегда равна одной денежной единице (1 доллар)
Хотя стандартные таблицы содержат для удобства все шесть функций, достаточно знать три основные, поскольку остальные три являются обратными по отношению к ним. Расчеты, требующие умножения, могут быть выполнены через деление на обратную величину, и наоборот (см. табл. 4-4).
Прочие соотношения
Сумма фактора фонда возмещения (колонка 3) и периодического процента равна взносу на амортизацию 1 долларов (колонка 6). Это соотношение показывает что взнос на амортизацию 1 долларов является суммой двух элементов. Первый элемент — процент, доход на инвестиции; второй — возмещение капитальных затрат, возврат инвестированных средств. Рассчитывая платежи по кредиту на основе взноса на амортизацию одного доллара, заемщики выплачивают в течение срока кредита основную сумму плюс процент. В том же случае, когда выплачивается лишь процент, однако основная часть долга не амортизируется вплоть до истечения срока кредита, заемщик может вносить в каждый период на отдельный счет определенную сумму, рассчитанную по фактору фонда возмещения. С учетом того, что фонд возмещения приносит процент по той же ставке, что и полученный кредит, по окончании срока последнего Остаток фонда возмещения может быть использован для погашения остатка задолженности.
ТАБЛИЦА 4-4
Базовые функции сложного процента и их обратные величины
| Функция | Обратная величина |
| Накопленная сумма единицы (колонка 1)
Накопление единицы за период (колонка 2) Текущая стоимость аннуитета (колонка 5) |
Текущая стоимость единицы (колонка 4)
Фактор фонда возмещения (колонка 3) Взнос на амортизацию единицы (колонка б) |
Взнос на амортизацию 1 долларов (колонка 6) соотносится со ставкой процента таким образом, что взнос должен всегда превышать периодическую ставку процента вне зависимости от срока кредита. В том же случае, если каждый платеж по кредиту не превышает обязательный периодический процент, кредит не будет погашен периодическими платежами.
Аналогично текущая стоимость обычного аннуитета (колонка 5) никогда не может превысить фактор, равный частному от деления 1 долларов на периодическую ставку процента. Например, если годовая ставка равна 10% (0,10), то максимальное значение фактора в колонке 5 будет 10 (1 долларов: 0,10 s 10). Максимальное значение фактора в колонке 5 при любой ставке процента показывает сумму, достаточную для генерирования 1 долларов за период на протяжении неограниченного времени. Остаток 10 долларов при 10%-ной ставке даст за год 1 долларов процента. Процент может быть использован по усмотрению вкладчика, не влияя тем самым на основную сумму вклада и генерируя бесконечный поток доходов. Табличные факторы текущей стоимости аннуитета, рассчитанные для конечного периода времени, будут стремиться к величине, равной отношению 1 долларов к периодической ставке процента, однако они никогда не смогут ее превзойти. Пример шестифакторной таблицы сложного процента показан в табл. 4-5.
Использование таблиц. Используя таблицы, аналитик должен ответить на следующие вопросы:
1. Уверены ли вы в том, что правильно понимаете задачу? Предусматривает ли ее решение использование накопления или дисконтирования? Не носит ли данная задача комбинированный характер, требующий использовать более чем одну функцию?
2. Не происходит ли накопление чаще, чем один раз в год, правильно ли вы выбрали эффективную ставку процента?
3. Когда происходят поступления или отток денежных средств — в начале или в конце каждого периода? Насколько это соответствует тому, как рассчитан соответствующий фактор в таблице? Возможно, что в него необходимо внести поправку.
4. Проверили ли вы правильность арифметических расчетов? Насколько полученное решение имеет смысл?
Шестифакторная таблица сложного процента
Таблица сложного процента номинальная годовая ставка = 10%, частота накопления (в год)=1
Расширение таблиц
Колонка 1 может быть расширена до любого числа лет или периодов путем перемножения факторов с тем, чтобы получить фактор, соответствующий заданному периоду. Данный расчет проводится путем сложения периодов до заданного числа и последующего перемножения соответствующих им факторов. Например, фактор за 80 лет при ставке 10% может быть рассчитан путем суммирования периодов и умножения 40-летнего фактора на него же самого (40 лет + 40 лет 80 лет; 45,2593 X 45,2593 = 2048,4); или сложением периодов и умножением 50-летнего фактора на 30-летний фактор (50 лет + 30 лет = 80 лет; 117,3909 X 17,4494 2048,4); или путем сложения периодов и умножения 30-летнего фактора на 22-летний и 28-летний факторы (30 + 22 + 28 80 лет; 17,4494 х 8,1403 х 14,42104 « 2048,4).
Колонка 4 может быть расширена таким же образом. Фактор за 80 лет при ставке 10% может быть рассчитан путем суммирования периодов и умножения фактора за 40 лет на него же самого (40 + 40 80; 0,0221 X 0,0221 = 0,0004884); или сложением периодов и умножением 50-летнего фактора на 30-летний фактор (50 лет + 30 лет = 80 лет; 0,0573 X 0,0085 = 0,000487). Разница связана с округлением результатов.
Колонка накопления единицы за период может быть расширена путем суммирования факторов накопленной суммы единицы в колонке, укороченной на один год. Например, для того чтобы рассчитать накопление единицы за одинадцать лет, следует прибавить накопленную сумму единицы за 10 лет к 10-летнему накоплению единицы за период. Колонка фактора фонда возмещения может быть расширена путем расчета величины, обратной накоплению единицы за период.
Расширение колонки 5 — текущая стоимость аннуитета — проводится путем суммирования факторов колонки 4 за будущие годы. Например, текущая стоимость аннуитета за 11 лет равна сумме 10-летнего фактора текущей стоимости аннуитета и текущей стоимости реверсии за 11 лет.
Поскольку взнос на амортизацию 1 долларов (колонка 6) является обратной величиной по отношению к текущей стоимости аннуитета, то данная колонка может быть расширена за счет нахождения соответствующих обратных величин.
Источник: Джек Фридман, Николас Орудей. Анализ и оценка приносящей доход недвижимости.