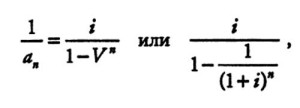Нередко кредиты структурированы таким образом, что платежи в их погашение в течение установленного периода времени превышают процент и позволяют полностью самортизировать кредит. Амортизацией (amortization) называется процесс погашения (ликвидации) долга с течением времени. Математически взнос на амортизацию кредита определяется как отношение одного платежа к первоначальной основной сумме кредита. Взнос на амортизацию единицы показывает, каким будет обязательный периодический платеж по кредиту, включающий процент и выплату части основной суммы и позволяющий погасить кредит в течение установленного срока.
В предыдущей главе было показано, что текущая стоимость 1 долларов, ожидаемого к получению в конце каждого года на протяжении четырех лет, при 10%-ной годовой ставке составляет 3,1698 долларов Первый 1 долларов будет стоить 0,90909 долларов, второй — 0,8264 долларов, третий — 0,7513 долларов, четвертый — 0,6830 долларов Сумма за четыре года равна 3,1698 долларов (0,90909 долларов + 0,8264 долларов + 0,7513 долларов + 0,6830 долларов 3,1698 долларов).
Взнос на амортизацию 1 долларов рассчитывается как величина, обратная полученному результату. Иначе говоря, при кредите в 3,1698 долларов под 10% годовых взнос на амортизацию дает ответ на вопрос: «Каков ежегодный платеж, необходимый для амортизации (погашения) этого кредита в течение четырех лет?» Ответ равен 1 долларов
Математическое отношение одного платежа к первоначальной основной сумме кредита составляет 1,00 долларов/3,1б98 долларов — 0,315477. Данный фактор — 0,315477, показывает величину периодического платежа, необходимого для погашения задолженности, т.е. для того чтобы полностью погасить долг (как его первоначальную ершу, так и начисляемые на остаток 10% годовых), на каждый доллар кредита по окончании каждого года в течение четырех лет необходимо выплачивать 0,315477 долларов Кредит в 100 раз больший потребует стократного увеличения регулярного платежа. Поэтому, если бы кредит составлял 316 000 долларов, то ежегодные выплаты по нему в течение четырех лет равнялись бы 100 долларов Для проверки используйте метод «депозитной книжки*, показанный в табл. 4-1.
ТАБЛИЦА 4-1
Метод «депозитной книжки» (сумма заемных средств = $316,98; ставка процента = 10%; ежегодный платеж а $100)
|
Год |
Остаток |
Плюс |
Минус выплаты |
Остаток, |
|
по кредиту |
процент (10%) |
процента и |
конец года | |
|
на начало года |
основной суммы |
|||
|
(в долларов) |
(в долларов) |
(в долларов) |
(в долларов) | |
|
1 |
316,98 |
+31,70 |
-100,00 |
=248,68 |
|
2 |
248,68 |
+24,87 |
-100,00 |
=173,55 |
|
3 |
173,55 |
+17,36 |
-100,00 |
=90,91 |
|
4 |
90,91 |
+9,09 |
-100,00 |
= 0 |
Зависимость суммы платежа от срока выплаты и ставки процента
Чем выше процентная ставка и/или короче срок амортизации кредита, тем выше должен быть обязательный периодический платеж. И наоборот, чем ниже ставка процента и более продолжителен срок выплат, тем ниже обязательный регулярный платеж. Каждый равновеликий взнос на амортизацию единицы включает процент (доход на инвестиции) и выплату части первоначальной основной суммы (возврат инвестиций). Соотношение этих составляющих изменяется с каждым платежом, как показано на рис 4-1.
Предварительно рассчитанные таблицы
Интенсивное и широкое использование фактора взноса на амортизацию одного доллара вызвало необходимость построения соответствующих таблиц. Некоторые таблицы сложного процента, как правило в колонке 6, показывают данный фактор в расчете на 1 долларов кредита. Другие же таблицы составляются в расчете на иные суммы кредита, обычно с шагом в 100 или 1000 долларов.
При составлении таблиц используется следующая формула, обратная формуле текущей стоимости аннуитета:
Взнос на амортизацию единицы
где
i — ставка процента;
п — число периодов;
Vn — текущая стоимость единицы;
ап — текущая стоимость аннуитета.
Для построения набора таблиц следует разделить единицу на текущую стоимость аннуитета. Расчет текущей стоимости аннуитета был описан в предыдущей главе.
Применение калькулятора
Для того чтобы использовать финансовый калькулятор при расчете обязательного периодического платежа по кредиту, введите число периодов N, ставку процента %1 и первоначальную сумму кредита PV. Затем нажмите COMPUTE и РМТ. На дисплее появится сумма периодического платежа, необходимого для амортизации кредита. Пример показан на рис. 4-2.
Укороченные интервалы
Многие кредиты предусматривают ежемесячные, поквартальные или полугодовые платежи. Для того чтобы учесть это, необходимо разделить номинальную годовую ставку процента на частоту накопления (например, при ежемесячном накоплении разделить на 12) и умножить число периодов в году на число лет (например, при ежемесячном накоплении умножить число лет на 12 для того, чтобы определить число периодов, на которые предоставляется кредит).
Источник: Джек Фридман, Николас Орудей. Анализ и оценка приносящей доход недвижимости.